
Il tuo browser non supporta il tag embed per questo motivo non senti alcuna musica
IX. Sulle 231 Porte delle Permutazioni delle Lettere
Quando Egli traccia, taglia, moltiplica, pesa e inverte le ventidue lettere, Egli crea qualsiasi cosa sia stata creata, e qualsiasi cosa che sarà creata in futuro. Come Egli è riuscito a moltiplicarle? Aleph [a] con ogni lettera e ognuna con Aleph, Beth [b] con ognuna e ognuna con Beth, e lo stesso per Ghimel [g]. Egli le gira e le inverte tutte, e forma una totalità di 231 parole. Tutte le creature e tutte le parole non possono esistere senza un essere superiore sopra di loro.
Ho tradotto le parole "hozerot halilah" come "Si rinnovano in un ciclo" poiché ogni cavità è così chiamata nella lingua Ebraica. Le parole "n'vuv luhot" ["cavità coperte", Esodo XXVII, 8] sono definite come "halil luhin" nel Targum. Si riferiscono agli orifizi del corpo, è detto: "Dio ha creato in esso molte aperture e cavità" [Berakhot 60 b]. Parafrasando, il Targum ha similmente detto del re di Tiro: "Ma tu non hai considerato che il tuo corpo è stato fatto con aperture e cavità che sono indispensabili" [parafrase di Ezechiele XXVIII, 13]. Allo stesso modo, la totalità dell’aria è chiamata "cavità del mondo" perché è sempre in movimento [circola].
Questo brano è talvolta mal compreso cioè: "Si rinnovano in un ciclo ed esistono in 221 porte", e questo non è corretto. Sebbene abbiamo appreso che il calcolo richiede che questo numero totalizza duecento trentuno, l’unico numero che ho visto scritto è "duecento ventuno". Non ho dubbi che questo sia un errore. Un errore simile può essere trovato in i Quattro Cancelli: "ogni Tishri di un anno embolistico che comincia prima di 695 parti della dodicesima ora". Ora, in tutti i testi che ho trovato, "l’11 ora" è scritta al posto della dodicesima, ma questo è un errore. Se si aggiunge l’eccedenza di due anni, uno dei quali è un anno embolistico, la nuova luna cadrà esattamente alle cinque in punto di Sabbath, anche se dovrebbe essere esattamente alle sei in punto. Non sarà alle sei, comunque, a meno che la dodicesima ora è stabilita come punto di partenza. Analogamente, in risposta alla domanda dell’autore, "Come le combinò", è corretto fornire il numero duecentotrentuno come risposta. Spiegherò ciò con il principio che applica lo stesso autore: "Aleph con tutte le lettere e tutte con Aleph, Beth con tutte e tutte con Beth", ecc. Questo tipo di moltiplicazione può essere trovata nelle città della Palestina e dell’Egitto. I ragazzi scrivono questo al fine di imparare come comporre, e queste sono le ventidue serie chiamate righe [file]. La prima riga è Aleph-Aleph, Aleph-Beth, Aleph-Ghimel, Aleph-Daleth, Aleph-Hé, Aleph-Vav, Aleph-Zayn, fino a Aleph-Tav. La seconda riga è Beth-Aleph, Beth-Beth, Beth-Ghimel, Beth-Daleth, Beth-Hé, Beth-Vav, Beth-Zayn fino a Beth-Tav. La terza riga è Ghimel-Aleph, Ghimel-Beth, Ghimel-Ghimel, Ghimel-Daleth, Ghimel-Hé, Ghimel-Vav, Ghimel-Zayn fino a Ghimel-Tav. É lo stesso per Daleth-Aleph, Hé-Aleph, fino a Tav-Aleph, Tav-Beth, Tav-Ghimel ecc., fino a Tav-Tav. In totale, questo risultato di ventidue per ventidue fa quattrocentottantaquattro. Da questo totale, devono essere sottratte ventidue parole che non sono prodotti [di una lettera con un’altra], vale a dire Aleph-Aleph della prima riga, Beth-Beth della seconda riga, Ghimel-Ghimel della terza, Daleth-Daleth della quarta, e così via fino a Tav-Tav della ventiduesima riga. La ragione di questa sottrazione è la seguente: se Daleth è combinata con Daleth, per esempio, semplicemente produce nell’aria la medesima figura e una singola parola nella voce, e rimangono nel loro stato originale quando sono invertite.
Una volta che abbiamo sottratto questi ventidue [duplicati], ci rimangono quattrocento sessantadue. Di queste quattrocentosessantadue, comunque, solo una metà sono effettivamente insiemi di coppie differenti. La coppia Aleph-Beth nella prima riga è come la coppia Beth-Aleph nella seconda; Aleph-Ghimel nella prima riga è come Ghimel-Aleph nella terza; Aleph-Daleth nella primaria è come Daleth-Aleph nella quarta, e così via per ognuna delle serie. Si scopre quindi che una metà delle lettere riproduce semplicemente l’altra metà, e così è detto: "Si rinnovano in un ciclo ed esistono in 231 porte" poiché ruotano nel loro inverso.
Se si sottrae la metà di quattrocentosessantadue, il resto è duecentotrentuno. Così abbiamo detto: Si rinnovano in un ciclo ed esistono in 231 porte". Una persona può avere una prova tangibile di tutto questo semplicemente calcolandolo con l’aiuto di monete o tracciando le righe di lettere e contandole (2). Ciò spiega come l’unità apparente su tutte le moltiplicazioni è un segno dell’Uno, il Santo, possa Egli essere glorificato ed esaltato!
Ho saputo che un commentatore del nostro libro ha mantenuto l’errore delle duecentoventuno porte. Egli ha tentato di giustificare questo errore dicendo che il totale di Aleph-Aleph, Aleph-Beth, Aleph-Ghimel, Aleph-Daleth e così via è solo ventuno poiché Aleph-Aleph non è moltiplicato [congiunto] e Aleph ruota solo su se stesso. Questo commentatore poi moltiplica questi ventuno per dieci, cioè, i dieci numeri, e il totale è duecento dieci. Poi egli aggiunge i dieci numeri e Aleph, che è la prima unità, e quindi l’ammontare è duecento ventuno. Ma, possa Dio avere pietà di te, questa è una catena di un intreccio di errori, tutti dovuti al fatto che il commentatore non conosce come moltiplicare. Possiamo citare cinque ragioni del perché la sua spiegazione è erronea:
1 - egli ha moltiplicato Aleph con tutte le lettere ma non tutte le lettere con Aleph. Più tardi egli ripete questo errore mancando di moltiplicare Beth con tutte o tutte con Beth, e lo stesso con le altre lettere. Egli ha solo moltiplicato Aleph con tutte;
2 - ha moltiplicato la soma di Aleph con tutte (ossia, ventuno) per dieci, ma non c’è ragione di moltiplicare per dieci. L’autore del nostro libro non ha dato questa indicazione. Ha soltanto indicato al ricercatore di moltiplicare le lettere, e dice "Aleph con tutte" e "Beth con tutte". Non ha indicato i dieci numeri in questa sezione. Il commentatore ha così omesso questa indicazione e ha fatto ciò che non era stato indicato;
3 - Ha indipendentemente aggiunto i dieci numeri a questo prodotto, ma questo è il capitolo sulla moltiplicazione e non sull’astrazione. Se questo fosse il capitolo sull’astrazione, si potrebbe aggiungere le ventidue lettere isolate, e questo porterebbe a duecento quarantatre;
4 - il commentatore ha omesso il doppio Aleph senza moltiplicarlo per dieci, e perciò deve aggiungere Aleph isolato, ma non c’è ragione per una tale procedura;
5 - questo libro del commentatore contiene anche la frase: "e tutte girano in circolo." Ora se le lettere sono moltiplicate l’una con l’altra, esse gireranno in circolo, ma non gireranno in circolo se sono semplicemente moltiplicate per dieci. Con ciò detto, mi piacerebbe sapere cosa rimane da difendere della tesi del commentatore.
L’obiettivo del nostro autore in questo capitolo sulla moltiplicazione è di dimostrare che il Creatore, possa Egli essere esaltato! componendo queste ventidue lettere tramite le cinque procedure, incidere, plasmare, combinare pesare e permutare ha creato tutto ciò che è stato e che esisterà in futuro. Attualmente, quando Egli ha tracciato linee dritte attraverso le circonferenze, triangoli nei quadrati, e disegnò linee oblique in queste circonferenze, triangoli e quadrati, i risultati furono superfici e volumi ripiegati uno sull’altro secondo questi meravigliosi metodi che creano tutte le forme. Questa è una penetrazione di Beth in Ghimel, Daleth in Hé, ecc. Per questa ragione, le coppie Aleph-Aleph, Beth-Beth, Ghimel-Ghimel, Daleth-Daleth fino a Tav-Tav non intervengono in questa moltiplicazione. Se si pronuncia Aleph un centinaio di volte, risulterà una sola forma nell’aria, letteralmente una linea dritta. E se si pronuncia Beth un centinaio di volte, si traccerà ripetutamente solo una singola forma circolare. Ciò spiega la creazione delle forme delle lettere nell’aria. Comunque, noi possiamo solo determinare questa forma nel nostro spirito. Non saremo in grado di realizzare questa forma perché appartiene al Padrone dei mondi, possa Egli essere glorificato ed esaltato! Il saggio, quindi, prima insegna ai suoi discepoli la matematica e la geometria, poiché queste sono le origini della conoscenza. [...]
X. Sull’Incoronazione delle Lettere:
Il riferimento ad ogni lettera, "Legò a lei una corona, la combinò con tutte le altre e la sigillò" si conforma ad un antico principio di felice memoria! Una tradizione relativa alle lettere è che esse sono state rivelate con ornamenti e corone, come è detto: "Sette lettere necessitano tre ornamenti: Shin, Ayin, Thet, Nun, Zayn, Ghimel e Tsadeh" [Menahot 29 b]. É lo stesso per ogni lettera. Per alcune lettere, questi ornamenti accrescono e per altri impediscono le deduzioni tracciate da esse, come il Libro delle Corone ha spiegato. Gli antichi seguono anche la tradizione secondo cui quando le corone non sono tracciate accuratamente nella Torah, è proibito pronunciare benedizioni su di essa, e non è permesso leggerla in pubblico. Per questa ragione, dicono anche che uno che la scorre velocemente non vivrà a lungo. Gli antichi fabbricanti di amuleti dicono che le lettere sono senza valore se non sono state scritte con le loro corone. Similmente, il nostro autore dice che non è possibile formare il triangolo, il quadrato, ripiegarli, unire in una catena, o creare figure convesse (che le lettere furono intese a formare) senza una corona. Egli dice, quindi, che "Legò a lei una corona, la combinò con tutte le altre e la sigillò"…
[2] L’autore giunge a questo risultato per via empirico-deduttiva. In realtà si tratta dell’applicazione di una semplice formula matematica. Per spiegarla richiamiamo alcuni semplici concetti. Si dice calcolo combinatorio il complesso delle procedure che permettono il conteggio dei vari tipi di raggruppamenti che possono essere formati scegliendo k elementi tra gli n elementi di un insieme assegnato. Nel caso esposto nel commento al Sepher Yetzirah, si tratta delle cosiddette "combinazioni semplici". "Dato un insieme di n elementi distinti si dicono combinazioni semplici di classe k i diversi sottoinsiemi formati con k elementi scelti tra gli n dati. Il numero di tali sottoinsiemi si indica con Cn,k". Le combinazioni si considerano diverse solo se hanno diversa composizione:
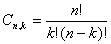
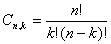
Nel caso del testo si ha:


Che è appunto il risultato trovato dall’autore [n.d.t.]